Non-reversible parallel tempering: a scalable highly parallel MCMC scheme

Abstract

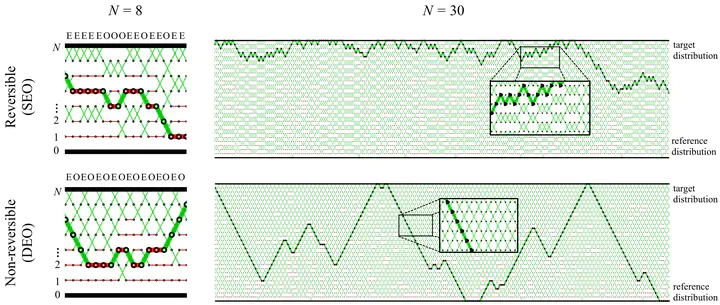
Parallel tempering (PT) methods are a popular class of Markov chain Monte Carlo schemes used to sample complex high-dimensional probability distributions. They rely on a collection of $N$ interacting auxiliary chains targeting tempered versions of the target distribution to improve the exploration of the state-space. We provide here a new perspective on these highly parallel algorithms and their tuning by identifying and formalizing a sharp divide in the behaviour and performance of reversible versus non-reversible PT schemes. We show theoretically and empirically that a class of non-reversible PT methods dominates its reversible counterparts and identify distinct scaling limits for the non-reversible and reversible schemes, the former being a piecewise-deterministic Markov process and the latter a diffusion. These results are exploited to identify the optimal annealing schedule for non-reversible PT and to develop an iterative scheme approximating this schedule. We provide a wide range of numerical examples supporting our theoretical and methodological contributions. The proposed methodology is applicable to sample from a distribution $\pi$ with a density $L$ with respect to a reference distribution $\pi_0$ and compute the normalizing constant. A typical use case is when $\pi_0$ is a prior distribution, $L$ a likelihood function and $\pi$ the corresponding posterior.