Local Exchangeability

Abstract

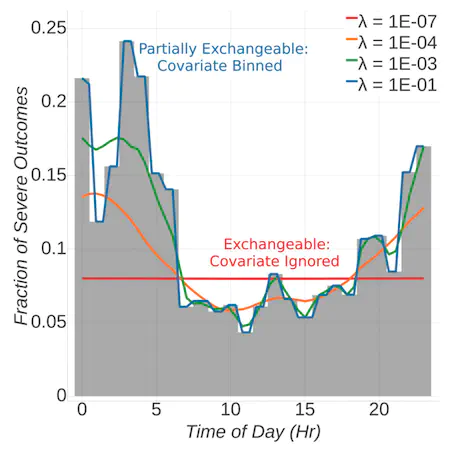
Exchangeability – in which the distribution of an infinite sequence is invariant to reorderings of its elements – implies the existence of a simple conditional independence structure that may be leveraged in the design of statistical models and inference procedures. In this work, we study a relaxation of exchangeability in which this invariance need not hold precisely. We introduce the notion of local exchangeability – where swapping data associated with nearby covariates causes a bounded change in the distribution. We prove that locally exchangeable processes correspond to independent observations from an underlying measure-valued stochastic process. Using this main probabilistic result, we show that the local empirical measure of a finite collection of observations provides an approximation of the underlying measure-valued process and Bayesian posterior predictive distributions. The paper concludes with applications of the main theoretical results to a model from Bayesian nonparametrics and covariate-dependent permutation tests.